Further developing approximation methods for linear inverse problems on spherical geometries with applications from the geoscience and medical imaging
Principal investigator: Prof. Dr. Volker Michel
Project manager/Main research: Dr. Sarah Leweke, Dr. Naomi Schneider
Title of research project: Further developing approximation methods for linear inverse problems on spherical geometries with applications from the geoscience and medical imaging
Funding: DFG MI 655/7-2, DFG MI 655/10-1/2, DFG MI 655/14-1
Project partners: Athanassios S. Fokas, Department of Applied Mathematics and Theoretical Physics, University of Cambridge, UK
Olaf Hauk, MRC Cognition and Brain Sciences Unit, Cambridge, UK
Karin Sigloch, Earth Science Department, University of Oxford and CNRS Geoazur, Université Côte d‘Azur
Nico Sneeuw, Geodätisches Institut, Universität Stuttgart
Project area: Mathematics
Cluster: Horus and Omni High Performance Clusters at the University of Siegen
Software: C/C++ and GSL, Julia, Matlab, NLopt
Introduction:
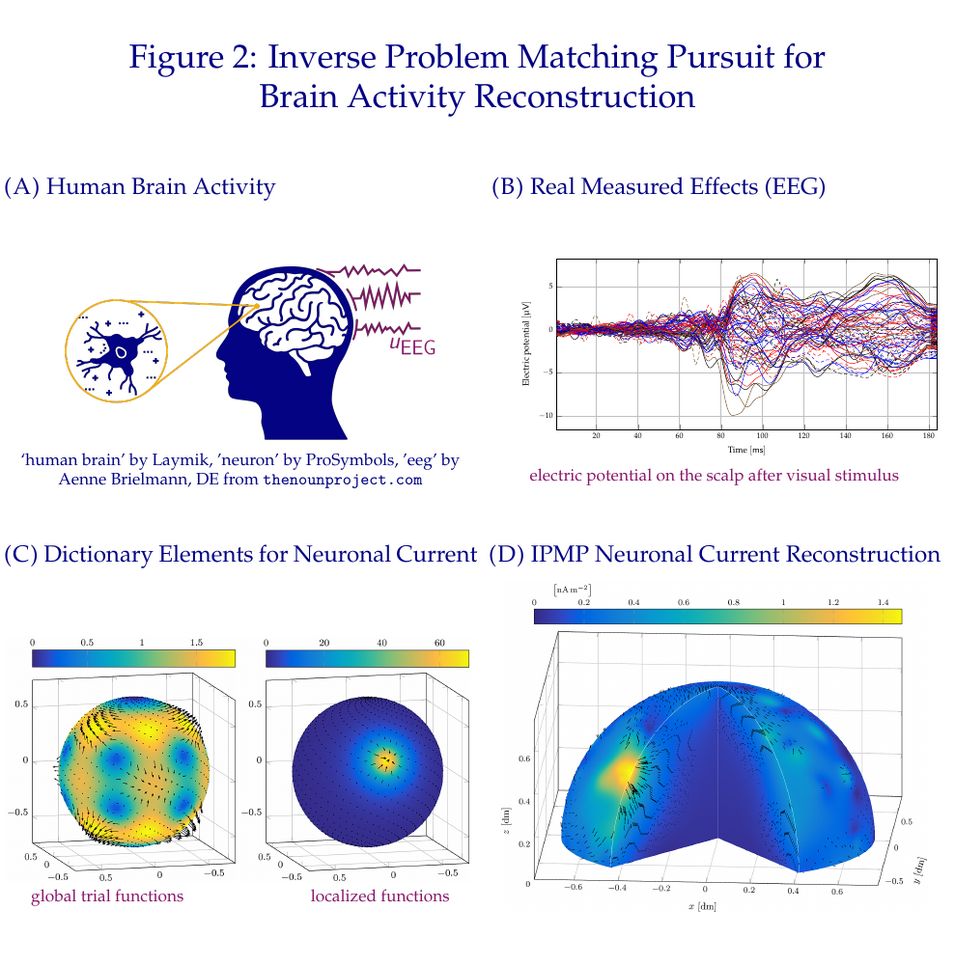
As geomathematicians, we are concerned with tasks like the downward continuation of the gravitational potential or the reconstruction of brain activity from MEG and EEG data. These are examples of inverse problems: the identification of a cause given its (measured) effects. Such problems have been extensively studied in Cartesian spaces. Most inverse problems in geoscience and medical imaging are illposed. That means, they present us with extraordinary theoretical and computational challenges induced by e.g. a loss of source information in the measurements or a high influence of noise on the approximation. Our tailor-made methods, the (Learning) Inverse Problem Matching Pursuits ((L)IPMPs), exploit the structure of spheres and balls while also tackle the ill-posedness. They enable us to track climatic changes (e.g. water mass transports) of the Earth or brain activities during neuroscientific experiments.
Methods:
We seek a function, e.g., the gravitational potential at the Earth’s surface or the electrical current in the brain. We know that this function is mapped to a finitedimensional data vector, e.g., the gravitational potential at points on a satellite orbit or the magnetic field at sensor positions. Despite the finite-dimensional data, our approximation shall be obtained as an expansion in continuous dictionary elements. A dictionary is an intentionally redundant set of trial functions such as spherical harmonics or radial basis functions. Thus, our approximation will likely consist of trial functions from different basis systems. This is done to combine the best of several worlds: usually, we include global functions and localized ones. The former represent general trends and the latter model details. With a suitable dictionary, our methods account for the spherical nature of the tasks. The expansion of the approximation is obtained iteratively. In every iteration, the dictionary element that best explains the mismatch of simulated and remaining measured data is chosen. Mathematically, this is implemented by minimizing the Tikhonov functional. The selected trial function is then added to the current reconstruction and its part in the data is removed. Iterating this greedy procedure, the methods yield a – in some sense – sparse representation of the cause of the inverse problem. The chosen dictionary elements constitute a best basis. Our group has also developed extensions, e.g., regularization, orthogonalization or accepting a near-best matching dictionary element, to this basic IPMP that improve its performance. However, these IPMPs rely on an a-priori chosen, finite dictionary. For practical purposes, such a dictionary is large and inefficient. To avoid the manual choice and to decrease the computational costs, we developed a learning add-on: in these LIPMPs, we use an infinite dictionary by modelling the minimization of the Tikhonov functional as a constraint non-linear optimization problem. The best basis of the LIPMPs can be used as a finite dictionary in the IPMPs.
Results:
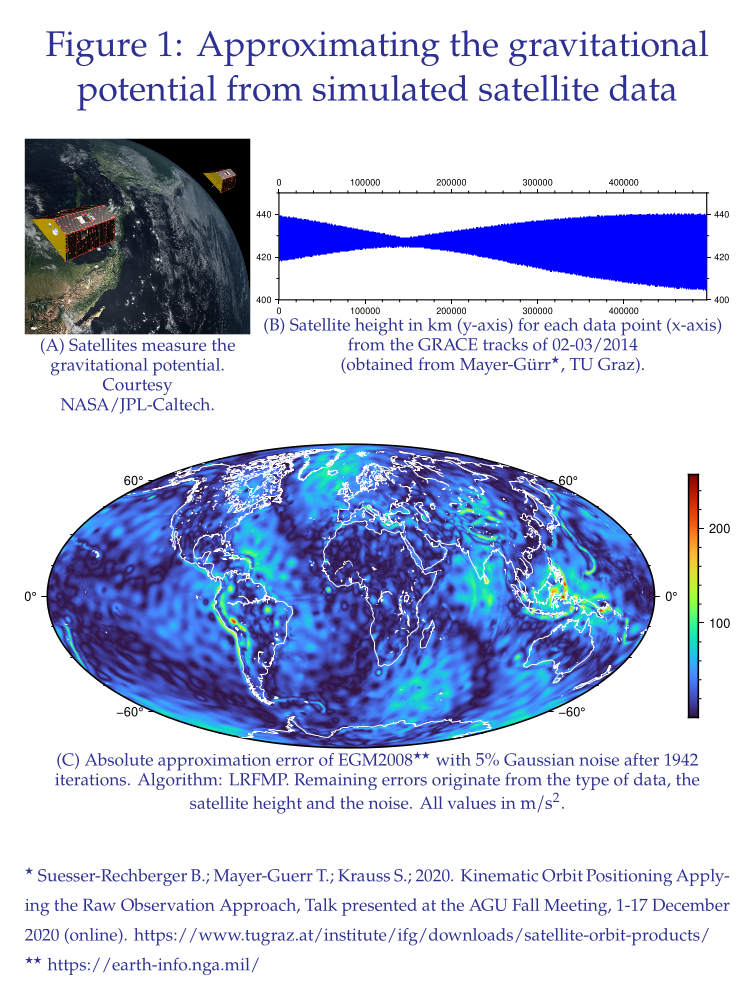
When equipped with problem-adapted regularizations, the methods successfully reconstructed neuronal currents inside the brain using sparse and irregularly distributed real data recorded during a clinical trial at the Cognition and Brain Science Unit, Cambridge, UK (Fig. 2(B)). From the downward continuation of the gravitational potential, we were in particular able to reconstruct local weather phenomena like the wet season in the Amazon basin. Recently, we were able to increase the number of used data points by a factor 40 up to 500.000 points (Fig. 1(C)).
Discussion:
Compared to standard techniques for inverse problems, the (L)IPMPs do not discretize the source or its domain. Moreover, they avoid to solve a large system of linear equations. Furthermore, all (L)IPMPs enable a joint inversion of data from different measurement techniques, e.g. satellite data and ground measurements. The preprocessing of a finite dictionary constitutes most of the runtime and/or storage demand. If we have many similar data sets, this is acceptable because the preprocessing is done only once in an offline phase and the values can be stored and re-used. However, due to the computational costs, we currently cannot quantify a possible bias introduced by a manual dictionary choice. Thus, if runtime, storage demand and/ or the choice of a dictionary poses a challenge, we advise to use the learning add-on.
Outlook:
First of all, we improve our experiment settings for the downward continuation of the gravitational potential in order to raise awareness in the geodetic community. The gravitational potential is important for climate studies. Secondly, we expand the set of applications by remodelling the (L)IPMPs for seismological travel time tomography. This aims at gaining more insight into, e.g., how tectonic plates behave below subduction zones. Thirdly, our goal is to facilitate the comparability of (L)IPMP results with established and upcoming inversion methods also in the field of MEG and EEG data inversion. Hence, we plan to provide an open-source software of the (L)IPMPs.
Sarah Leweke. 2018. The Inverse Magneto-electroencephalography Problem for the Spherical Multiple-shell Model – Theoretical Investigations and Numerical Aspects. PhD thesis. Geomathematics Group, University of Siegen. http://dokumentix.ub.uni-siegen.de/opus/volltexte/2019/1396/
Sarah Leweke, Volker Michel and Athanassios S. Fokas. 2020. Electro-Magnetoencephalography for the spherical multiple-shell model: novel integral operators with singular-value decompositions. Inv. Probl., 36 (2020), 035003. https://doi.org/10.1088/1361-6420/ab291f
Volker Michel and Sarah Orzlowski. 2017. On the convergence theorem for the regularized functional matching pursuit (RFMP) algorithm. Int. J. Geomath., 8 (2017), 183–190. https://doi.org/10.1007/s13137-017-0095-6
Volker Michel and Naomi Schneider. 2020.A first approach to learning a best basis for gravitational field modelling. Int. J. Geomath., 11 (2020), article 9. https://www.doi.org/10.1007/s13137-020-0143-5
Naomi Schneider. 2020. Learning Dictionaries for Inverse Problems on the Sphere. PhD thesis. Geomathematics Group, University of Siegen. http://dx.doi.org/10.25819/ubsi/5431
Naomi Schneider and Volker Michel. A dictionary learning add-on for spherical downward continuation. submitted to J. Geod. First version available at http://arxiv.org/abs/2012.05560
Naomi Schneider and Volker Michel. 2020. Dictionary learning algorithms for the downward continuation of the gravitational potential. Presented at the EGU2020: Sharing Geosciences Online. https://doi.org/10.5194/egusphere-egu2020-2367