Machine learning based approaches for combinatorial optimization problems
Principal investigator: Prof. Dr. Kevin Tierney
Researchers: André Hottung
Title of research project: Machine learning based approaches for combinatorial optimization problems
Project endurance: Sep 2019 - Today
Project area: Wirtschaftswissenschaften (112)
Cluster: GPU Cluster Bielefeld
Software: PyTorch
Introduction:
The long-term success of any business depends on the quality of decisions that are made in day-to-day operations. How many products should be produced on what machines? In which order should the products be delivered, and in which trucks? The field of operations research is concerned with methods that solve these combinatorial optimization problems. Operations research experts model problems and design complex solutions approaches to provide decision support to decision makers. However, the development of problem-specific solution algorithms is a very time intensive process. Hence, for many decision problems, it is not financially viable to solve them using state-of-the-art operations research techniques. Thus, suboptimal decisions are often being made and resources are wasted. In this research project, we focus on methods the can automate the design of powerful solution approaches to democratize optimization algorithms so that it is easier and more cost efficient to solve combinatorial optimization problems.
Methods:
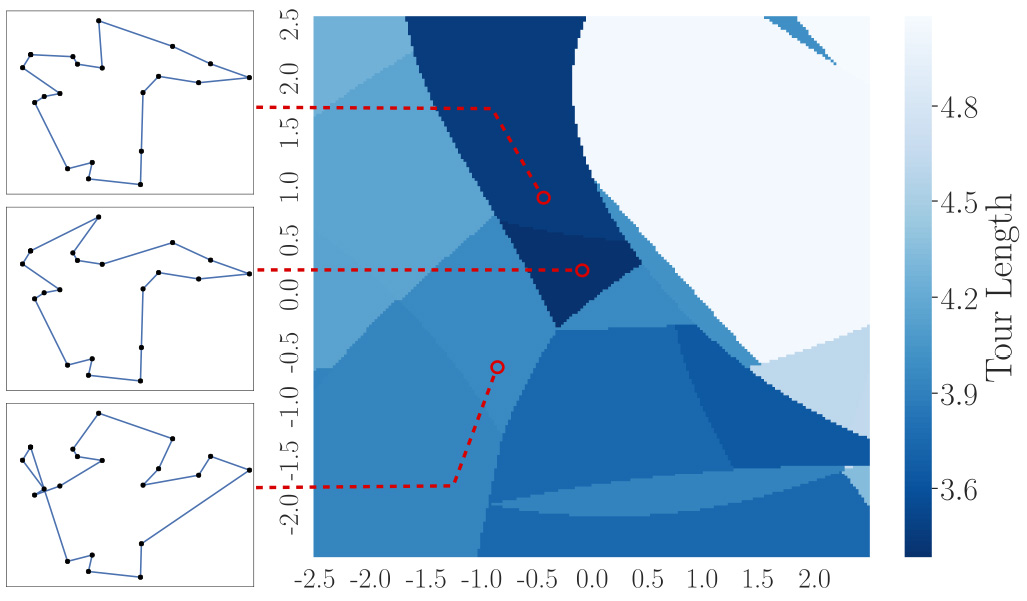
We developed multiple learning based approaches for combinatorial optimization problems. All our approaches require a representative set of problem instances that are used during the training of the employed deep neural networks. For example, in the publication “Learning a Latent Search Space for Routing Problems using Variational Autoencoders” we train a deep neural network to map discrete routing problem solutions to continuous space (Figure 1). The learned continuous space can then be searched by a problem-independent continuous optimization method. In the publication “Efficient Active Search for Combinatorial Optimization Problems” we use deep reinforcement learning as a high-level search procedure. In this approach, a deep neural agent repeatedly tries to solve a single given problem instance. Based on the quality of the found solution, the behavior of the agent is modified after each iteration with the objective of increasing the likelihood of generating high-quality solutions.
Results:
We evaluate our learning based methods on well-known optimization problems from operations research (e.g., on the traveling salesperson problem). Our methods have achieved excellent performance, and are already able to outperform some established operations research methods. For example, on capacitated vehicle routing problems we are able to outperform the well-established heuristic solver LKH3.
Discussion:
Especially for practical applications, learning-based approaches for optimization problems are of great interest because of the high labor costs associated with the development of handcrafted solution approaches. In the future, self-learning approaches could allow for better decision-making in a wide area of applications. Their learning-capabilities allows them to directly adapt towards those optimization problems that a business is facing.
Outlook:
In future work, we will investigate how learning-based methods can be easily applied to very complex optimization problems that have many side constraints. Finding solutions to these problems can be very challenging even for problem-specific, handcrafted approaches.
- HOTTUNG, A.; TIERNEY, K. 2020. Neural Large Neighborhood Search for the Capacitated Vehicle Routing Problem. ECAI. IOS Press, S. 443-450.
- HOTTUNG, A., BHANDARI, B, TIERNEY, K. 2021. Learning a Latent Search Space for Routing Problems using Variational Autoencoders. International Conference on Learning Representations.
- HOTTUNG, A., KWON, Y. TIERNEY, K. 2021. Efficient Active Search for Combinatorial Optimization Problems. arXiv preprint arXiv:2106.05126, 2021.